In part I of this post, I described how to detect and locate a Sudoku grid in the image, and then finding all the grid locations where the numbers and gaps are. This post is therefore about recognizing the numbers and gaps, solving the Sudoku (i.e. finding the numbers that should go in each gap), and finally project the solved numbers in the image gaps (aka augmented-reality style).
You can download the full code from GitHub, here I’ll just highlight the main parts to understand the algorithm. Please note that the proposed algorithm is not the optimal in a lot of senses, since it’s been designed as an academic tutorial that one can understand without a lot of knowledge about computer vision. This has left out some powerful but more advanced techniques.
1. Digit and gap recognition
Now that we have located the grid in the image and all its spots, let’s isolate every sub-image containing the digits to scan them using an OCR. First of all, we isolate and crop the whole image of the Sudoku Grid.
/* Get the image of the Sudoku full box
* by getting the first and last grids
* - ulx: Up Left X
* - uly: Up Left Y
* - drx: Down Right X
* - dry: Down Right Y */
unsigned int ulx = round(min(corners[0][0].x,corners[9][0].x));
unsigned int uly = round(min(corners[0][0].y,corners[0][9].y));
unsigned int drx = round(max(corners[0][9].x,corners[9][9].x));
unsigned int dry = round(max(corners[9][0].y,corners[9][9].y));
/* This is to be robust against some degenerate cases */
if(ulx>sx or uly>sy or drx>sx or dry>sy)
continue;
/* Crop the image */
Mat sudoku_box(frame_gray, cv::Rect(ulx, uly, drx-ulx, dry-uly));Here how an original frame looks like in practice:

And here the automatically cropped image showing the Sudoku grid:
We now proced to binarize the image using local thresholding, which is robust to local shadings. We could apply the OCR directly to this image and let it decide the binarization, but we found that binarizing the image ourselves worked better.
/* Apply local thresholding */
Mat sudoku_th = sudoku_box.clone();
adaptiveThreshold(sudoku_box, sudoku_th, 255,
CV_ADAPTIVE_THRESH_GAUSSIAN_C,
CV_THRESH_BINARY_INV, 101, 1);Here the grid after binarization:

As we can see, the grid is not perfectly aligned. That’s why we reduced the size of the small boxes in previous steps. We can now cut the thresholded image on each of the small boxes detected in the previous post and here we have some results:

Now that we have the binarized sub-images of the grid, let’s run the OCR on them.
/* Process all boxes and classify whether
* - They are empty (we'll say 0) or
* - There is a number 1-9 */
vector<vector<unsigned int>> rec_digits(9,vector<unsigned int>(9));
for(std::size_t ii=0; ii<9; ++ii)
{
for(std::size_t jj=0; jj<9; ++jj)
{
/* Get the square as an image */
Mat digit_box(sudoku_th, cv::Rect(
round(boxes[ii][jj].first.x)-ulx,
round(boxes[ii][jj].first.y)-uly,
round(boxes[ii][jj].second.x-boxes[ii][jj].first.x),
round(boxes[ii][jj].second.y-boxes[ii][jj].first.y)));
/* Recognize the digit using an OCR */
rec_digits[ii][jj] = recognize_digit(digit_box, tess);
}
}
/* Function to recognize a digit in a binarized image using Tesseract
* Note that we should limit Tesseract to look for digits only,
* but I didn't manage to do it from the C++ API... :)
* That's why we need to handle the 'I' as a '1', er similar...
*/
unsigned int recognize_digit(Mat& im, tesseract::TessBaseAPI& tess)
{
tess.SetImage((uchar*)im.data, im.size().width, im.size().height,
im.channels(), (int)im.step1());
tess.Recognize(0);
const char* out = tess.GetUTF8Text();
if (out)
if(out[0]=='1' or out[0]=='I' or out[0]=='i' or out[0]=='/'
or out[0]=='|' or out[0]=='l' or out[0]=='t')
return 1;
else if(out[0]=='2')
return 2;
else if(out[0]=='3')
return 3;
else if(out[0]=='4')
return 4;
else if(out[0]=='5' or out[0]=='S' or out[0]=='s')
return 5;
else if(out[0]=='6')
return 6;
else if(out[0]=='7')
return 7;
else if(out[0]=='8')
return 8;
else if(out[0]=='9')
return 9;
else
return 0;
else
return 0;
}Here the results of the recognition of the numbers present in the image.
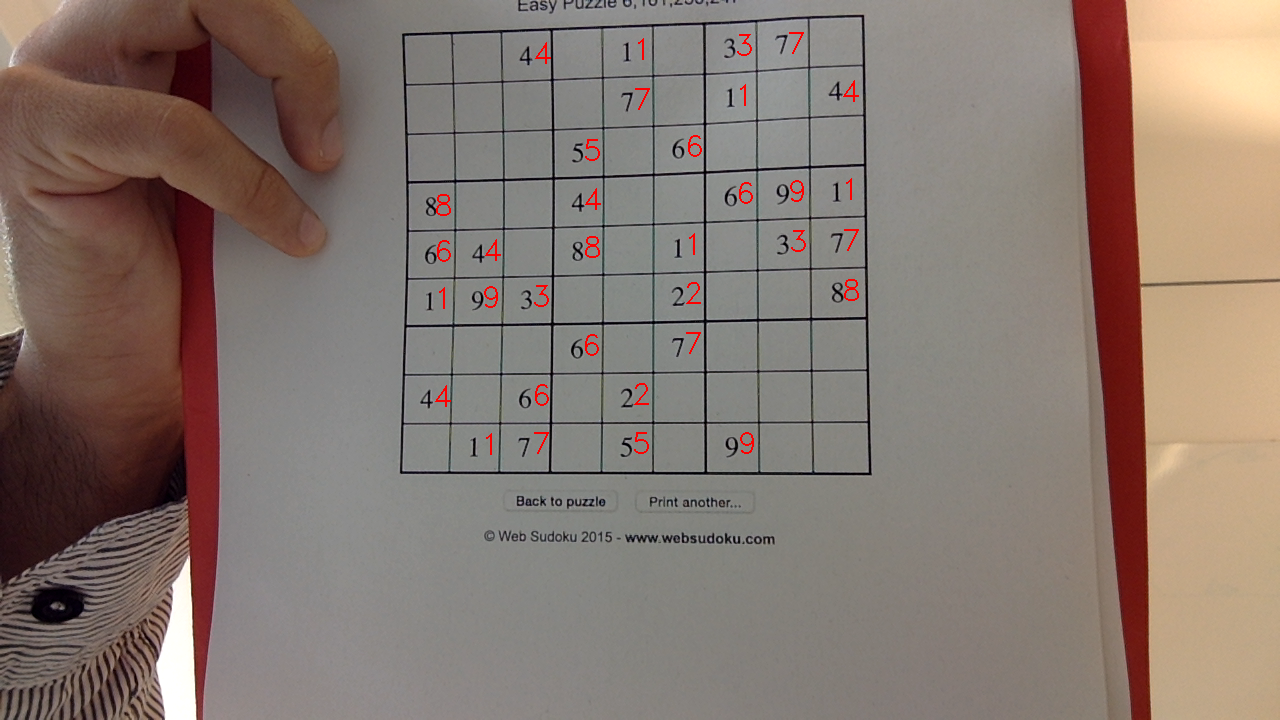
2. Solving the Sudoku
We now have all available digits recognized and we also now where the gaps are, so the next step is to solve the Sudoku. To do so, we create a class Sudoku, that mainly contains all the possible digits that are still possible at each grid location and a set of constraints that define the rules of Sudoku (there cannot be repeated numbers in a row, column, etc.).
/* Class that contains and solves the Sudoku of N*N*N
* grid 'spaces', i.e., the usual Sudoku is N=3 */
template<std::size_t N>
class Sudoku
{
/* Set of constraints container */
std::vector<Constraint> constraints;
/* Container of all possible numbers at each grid position */
std::vector<std::vector<std::unordered_set<char>>> grid;
}The first step is therefore to ingest all recognized digits into the Sudoku class, and then call to the solve function. The global call to the code would therefore be:
/* Create the Sudoku class */
const int N = 3;
Sudoku<N> sudoku;
/* Set the recognized digits */
for(std::size_t ii=0; ii<N*N; ++ii)
for(std::size_t jj=0; jj<N*N; ++jj)
sudoku.set_value(ii, jj, rec_digits[ii][jj]);
/* Let's try to solve it */
if(sudoku.solve())
std::cout << "We solved it!" << std::endl;The set_value() function reduces the possible values of that location to only one value, so that grid location is solved.
We will know that a Sudoku is solved, therefore, when all locations have only a single possible value, as the code below checks.
/* Function to check whether the Sudoku is solved,
* i.e., whether there is only one option left at all positions */
bool is_solved()
{
bool is_sol = true;
for(std::size_t ii=0; ii<N*N; ++ii)
for(std::size_t jj=0; jj<N*N; ++jj)
if(container[ii][jj].size()!=1)
{
is_sol = false;
ii = N*N;
jj = N*N;
}
return is_sol;
}So, now that we know whether the Sudoku is solved at a given stage, and we have set all the initial recognized digits, we would proceed by scanning all constraints iteratively and removing all solved numbers from the rest of positions possible values. After some iterations, we will be reducing the possible values in each location, until only one possibility remains. The global algorithm to solve the Sudoku would therefore be the following.
/* Function to solve the Sudoku, given the current imposed digits */
bool solve()
{
std::size_t max_iterations = 1000;
std::size_t n_iters = 0;
while(not is_solved())
{
/* Scan all constraints */
for(auto constr:constraints)
/* We impose that cosntrain, removing solved digits
* from the rest of locations in the constraint */
constr.scan_and_impose(grid);
n_iters++;
if(n_iters>max_iterations)
return false;
}
return true;
}This solving strategy is the most basic possible, and will therefore only solve the easy puzzles. In other words, we could keep end up iterating through all constraints without being able to change the possible numbers on each grid.
We would therefore be left with some positions with more than one possible number.
A possible way to proceed would be to do branching, that is, to take a location with a few possible numbers and make a guess among them. Then try to solve imposing that guess and if we are not able to solve keep trying with another guess. Obviously, this branching can also be nested. We leave this solution to the reader :).
3. Implementing constraints using Object-Oriented programming
Let’s implement the classes to impose the constraints in the Sudoku.
In generic, a constraint is a set of positions in the Sudoku grid, where there cannot be duplicate digits, for example a row or a column.
Let’s therefore create a generic class (subclass of Sudoku) that implements the algorithm to enforce this constraint.
We will then need to particularize the class to three types of constraints: rows, columns, and blocks.
They will be different only in how we define the coordinates covered by the constraints, but will share the code of how to impose them.
In Object-Oriented programming, we can implement this idea with a generic parent class that we will then specialize by class inheritance into three new classes.
Let’s delve into creating the generic parent class that implements a constraint.
/* Generic class that implements a constraint, i.e.,
* a set of positions where there cannot be any repeated number.
* We will implement the generic features of a constraint
* (scan all positions and impose no repetitions),
* and then we will specialize this class to the three types of
* constraints in a Sudoku (row, column, and block). This way,
* we don't have to duplicate code (Object-Oriented programming :)
*/
struct Constraint
{
/* Default constructor - Allocate containers
* We get 'N' from the mother class Sudoku */
Constraint(): row_coords(N*N), col_coords(N*N)
{
}
/* String identifying the constraint, for debugging purposes */
std::string id;
/* Coordinates of the constraint, that is, the positions
* where the constraints must be fulfilled */
std::vector<std::size_t> row_coords;
std::vector<std::size_t> col_coords;
/* Scan the constraint, find those positions with only one possible
* value, and erase the value from the rest of sets,
* where it cannot be.
* Example: If we find a place where '9' is the only possible
* number, we erase '9' from the list of possibilities in
* the other locations */
bool scan_and_impose(std::vector<std::vector<std::unordered_set<char>>>& contain)
{
[...]
}
};As you can see, it’s mainly a list of coordinates and a function to impose this constraint given a specific state of the Sudoku grid (you can see the full implementation in the code).
Every time we impose this constraint, we will be removing all digits that are solved in a certain position from the rest of locations.
Now that we have the generic constraint, we need to provide easy ways of filling the coordinates of the constraints, to avoid having to manually define them all.
We exemplify it, for instance, with the row constraint RowConstraint.
We inherit from the generic class Constraint and we specialize the constructor to take the specific number of row and fill the coordinates accordingly.
We also initialize the identifier string for debugging.
/* Specialized class for row constraints */
struct RowConstraint: public Constraint
{
/* Constructor receiving the particular row */
RowConstraint(std::size_t row)
{
/* Fill in all the coordinates of the row */
for(std::size_t ii=0; ii<N*N; ++ii)
{
this->row_coords[ii] = row;
this->col_coords[ii] = ii;
}
/* Set the identifier string */
std::stringstream ss;
ss << row;
this->id = "Row "+ss.str();
}
};Note the use of this-> to get access to the fields defined in the parent generic class.
With this class structure, the definition of the full set of constraints is reduced to the following constructor in the Sudoku class.
/* Default constructor, which:
* - Allocates the grid (N*N x N*N, e.g. 9x9)
* - Defines the N*N constraints of each type (e.g. 9 columns, etc.)
*/
Sudoku() : grid(N*N,std::vector<std::unordered_set<char>>(N*N))
{
for(std::size_t ii=0; ii<N*N; ++ii)
{
constraints.push_back( ColConstraint(ii));
constraints.push_back( RowConstraint(ii));
constraints.push_back(BlockConstraint(ii));
}
}4. Agumented-reality result display
Once the Sudoku is solved, the only remaining step is to reproject the solved digits into the gaps of the original Sudoku.
/* Plot the solved numbers in the gaps using augmenting reality */
for(std::size_t ii=0; ii<9; ++ii)
{
for(std::size_t jj=0; jj<9; ++jj)
{
/* Paint only the digits in the gaps of original Sudoku */
if (rec_digits[ii][jj]==0)
{
Point text_pos(boxes[ii][jj].first.x +(boxes[ii][jj].second.x-boxes[ii][jj].first.x)/5,
boxes[ii][jj].second.y-(boxes[ii][jj].second.y-boxes[ii][jj].first.y)/5);
stringstream ss;
ss << (int)processed_sudoku.get_value(ii,jj);
putText(frame, ss.str(), text_pos,
CV_FONT_HERSHEY_DUPLEX, /*Size*/1,
Scalar(0,0,255), /*Thickness*/ 1, 8);
}
}
}You can find the code from this blog post in GitHub.
And here the link to the final result video. If you liked this post or used the code, why don’t you say hi in the comments? :)

